
张志强,男,副教授,现任郑州商学院智能建造学院专任教师。2011年毕业于湘潭大学物理学院。主讲《大学物理》《大学物理实验》《生活中的物理学》《数学建模》等课程。主持省级教学工程研究性教学示范课程1门,建成校级精品在线开放课程1门。获河南省教学技能竞赛二等奖、信息技术与课程融合优质课大赛一等奖,并被评为河南省文明教师、郑州地方高校优秀中青年骨干教师。科研方面,发表论文25篇,其中第一作者SCI论文7篇、中文核心及CSCD论文8篇;主持、参与项目15项,含省科技攻关项目1项、教育厅高校重点科研项目3项。指导学生参加数学建模竞赛获全国大学生数学建模竞赛省级一等奖3项、美国大学生数学建模竞赛二等奖1项等多项荣誉。
想象一下,你是一位土木工程师,正在设计一座大桥的桥墩。河水奔流而过,尤其在洪水季节,水流会变得异常湍急、混乱,形成许多漩涡。这些水流会对桥墩产生巨大的冲击力和脉动压力,如果设计不当,桥墩可能会被破坏。那么,我们如何精确地预测这种复杂水流的形态和力量呢?
这背后离不开一个强大的工具——数值模拟。我们可以把它理解为在计算机里建立一个“数字河流”,通过数学方程来模拟真实的水流。而今天我们要介绍的,就是一个描述这种粘性流体(比如水)运动和冲击波的关键数学模型——耦合Burgers方程。
张志强老师与合作者在武汉大学学报自然科学英文版上发表了题为《The Space-Time Semi-Analytical Meshless Methods for Coupled Burgers' Equations》的文章中,提出了一种简单的半解析直接时空无网格格式用于耦合Burgers方程的数值近似求解方法。在求解过程中,考虑了径向基函数和非径向基函数两种不同的方案。数值结果表明,所提出的无网格方法精度良好、使用友好,并能有效地求解耦合的Burgers方程。文章链接为:https://doi.org/10.1051/wujns/2024296572。

图1 文章首页
01.传统方法的“烦恼”:时空的枷锁
在以前,科学家们用传统数值方法(网格法Mesh,如有限元法FEM,多重网格法multigrid method等)来求解这个方程时,遇到了两大难题:
1.“分步走路”的局限:传统方法就像我们看电影时一帧一帧地播放。它必须先把时间“切碎”,计算完一个时间点,再基于这个结果计算下一个时间点。这种方式不仅计算量大,更重要的是,每一步的微小误差会不断累积,就像走路时每一步都偏一点,最后会偏离目的地很远。尤其是在模拟高雷诺数(可以简单理解为水流非常湍急)的情况时,计算很容易变得不稳定甚至“崩溃”。
2.“画网格”的麻烦:传统方法需要在复杂的计算区域里“画网格”,就像给一个不规则的地块划分田埂。对于桥墩这种不规则形状,生成高质量的网格本身就非常耗时费力。如果水流导致边界动态变化,网格还需要重新划分,更是难上加难。
后来,虽然出现了不需要网格的“无网格方法”(Meshless),但它们依然没有摆脱“时间步进”的束缚,计算效率的提升有限。
02.考虑物理联系的“时空魔法”新方法
面对这些挑战,张志强老师的研究团队提出了一种非常巧妙的新思路——时空半解析无网格方法。这个方法的核心思想可以用一个词概括:时空一体化。
1.什么是时空一体化?
想象一下,通常认为世界是三维的(长、宽、高)。传统方法把时间当作一个独立的指挥官,在三维空间里一步步指挥。而新方法则认为,时间就是第四个维度!它将时间和空间放在完全平等的地位上,构建了一个包含时间轴的“四维时空坐标系”来处理问题。
基于这个革命性的想法,设计了两种神奇的“魔法工具”,即两种新型基函数:
方案一:简单粗暴的融合:径向基函数
这种方法把时间直接当作一个普通的空间维度来处理,构建出“各向同性”的基函数。你可以理解为,在它看来,时间方向和空间方向没有区别,用一套统一的规则在四维时空里“铺开”计算。这种方法形式简单,易于实现。
方案二:尊重物理的智慧:非径向基函数
这种方法更聪明一些,它意识到时间和空间在物理本质上毕竟不同。因此,它在构建基函数时,特意考虑了时间变量和空间变量之间真实存在的物理关系,使得构建出的数学工具更贴合流体运动的实际规律,理论上精度更高。
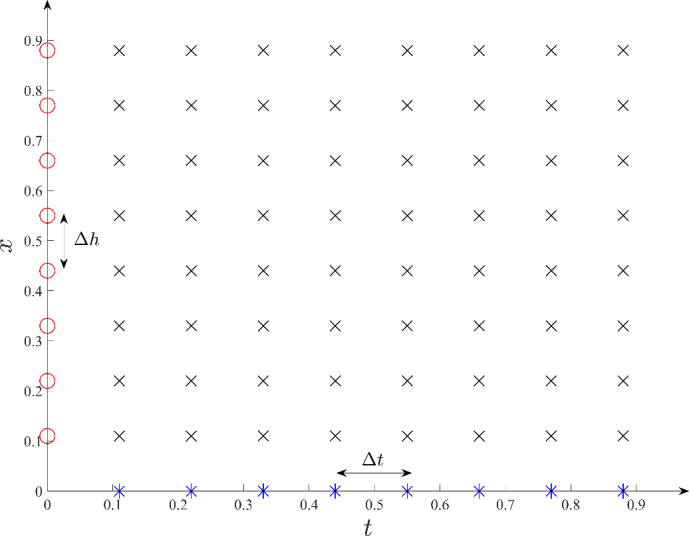
图2 时空坐标系配置
2.如何施放“魔法”?
在整个“时空区域”,包括初始时刻、边界位置和内部区域中选取一系列关键点,也称之为 “配点”。然后,将问题的近似解表示为那些新型基函数的线性组合,最后通过求解一个线性方程组,就能一次性得到整个时空区域内所有位置、所有时刻的流体状态。
03.魔法的威力:算得更快、更准、更稳
通过数值实验,这种新方法展现出了令人惊叹的优势:
1.效率飙升:因为它是一次性求解,避免了繁琐的时间迭代,计算效率比传统方法提升了约40%。这意味着以前需要算1个小时的问题,现在可能30多分钟就能搞定。
2.精度跃升:在一个测试案例中,新方法的绝对误差比传统方法降低了近5倍,也就是精度提高了5倍。在另一些关键位置和时刻,其计算误差甚至比传统方法低了1到2个数量级。
3.稳定性强:这种方法在模拟高雷诺数的流体,即流速非常高时,依然能保持稳定,克服了传统方法的一大痛点。
4.省时省力:最让人惊喜的是,即使用比较“粗糙”的配置点,新方法也能达到传统“细密”网格才能达到的精度。这大大减少了前处理的工作量和计算资源消耗。
04.这项研究与土木工程的未来
这项看似抽象的数学方法研究,对土木工程领域有着实实在在的巨大潜力:
1.更精准的水力预测:可以用于模拟洪水冲击桥梁、堤坝,或者城市排水管网中的复杂水流,帮助工程师设计出更安全、更经济的结构。
2.污染物扩散模拟:可以高效预测事故中泄漏的污染物在河流或地下水中的迁移路径和扩散过程,为环境应急提供决策支持。
3.扩展至其他领域:这种“时空一体化”的思路是通用的,同样可以应用于模拟地震波在土壤和结构中的传播(弹性波方程),或者大体积混凝土浇筑时的水化热传导(瞬态热传导方程)。这些都是土木工程中的核心问题。
这项研究,就像是为复杂流体问题的求解开辟了一条“时空快车道”。它打破了时间和空间的藩篱,通过构建新型的数学“魔法工具”,实现了一次性、全时空的同步解析。这不仅让我们算得更快、更准,也为我们未来解决土木工程中更多更复杂的科学问题,提供了全新的思路和强大的工具。未来,结合人工智能算法对参数进行自动优化,这套方法的威力还将进一步释放。这,正是基础科学研究推动工程技术进步的生动体现。

图3 本文入选2024年度湖北省科技期刊优秀百篇论文
值得一提的是, 8月26日,湖北省科学技术协会指导、湖北省科学技术期刊编辑学会组织实施的2024年度湖北省科技期刊优秀百篇论文遴选结果正式揭晓,本论文成功入选!
(文/詹缘梦 图/孙岚玥)

